horust

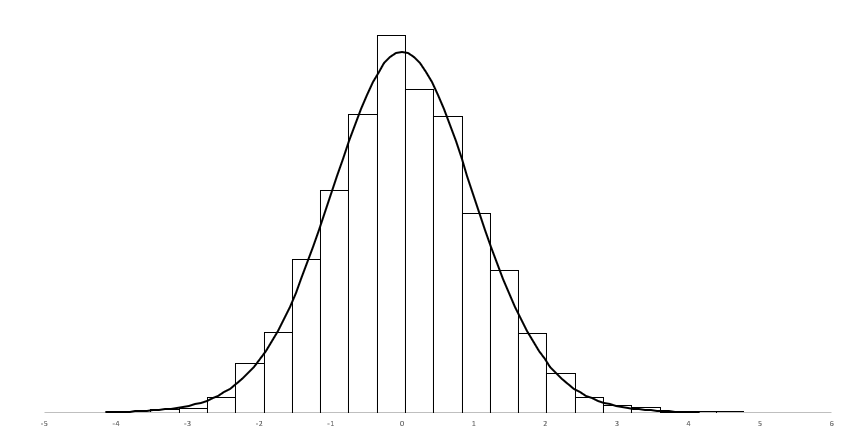
회귀 계수 $\widehat{\beta}_1$은 관찰된 표본에서 나온 값입니다. 회귀 계수를 구해 보면 당연히 표본마다 다를테지만 기대값이 있을 것이고 그 값을 중심으로 흩어져 있을 것입니다. 회귀 계수의 기대값과 분산을 구해 보면 다음과 같습니다(주석 (1)).$$\begin{aligned}E(\widehat{\beta}_1)&=\beta_1\\Var(\widehat{\beta}_1)&=\frac{\sigma^2}{\sum(x_i-\overline{x})^2}\end{aligned}$$그리고 회귀 계수 $\widehat{\beta}_1$는 정규 분포를 따른다고 합니다. 회귀 계수는 $x$가 변할 때 $y$가 변하는 정도인데 $x$는 상수 취급이고 $y$가 정규 분포를 따르니까 그런 것 같기는 합니다.$..

회귀 분석(regression analysis)은 두 변수들 사이의 확률적 관계를 알아 보는 분석입니다. 알아 보려는 그 관계가 선형이라면 선형(linear) 회귀 분석이라고 합니다. 두 변수 $x$와 $y$가 완벽한 선형의 관계라면 $y=\beta_0+\beta_1x$의 꼴로 표현할 수 있겠습니다. 그런데 $x$와 $y$가 확률적 관계라면 $y$ 값은 확률적으로 결정될 것이고 완벽한 선형일 때와 비교하면 오차(error)가 있을 겁니다. 따라서 두 변수의 관계는 다음의 모형으로 표현할 수 있습니다.$$y=\beta_0+\beta_1x+\varepsilon$$여기서 $\varepsilon$이 오차를 의미하는 확률 변수입니다. $\varepsilon$은 엡실론이라고 읽습니다. $x$가 어떤 값이 되든 오차..

t-분포확률 변수 $x$가 표준 정규 분포를 따르고, 확률 변수 $y$는 자유도가 $\nu$인 카이 제곱 분포를 따른다고 할 때, 확률 변수 $\frac{x}{\sqrt{y/\nu}}$는 자유도가 $\nu$인 t-분포(t-distribution)를 따른다고 합니다. $$x \sim N(0,1)$$$$y \sim \chi_{\nu}^2$$$$t=\frac{x}{\sqrt{y/\nu}} \sim t_{\nu}$$t-분포는 표준 정규 분포와 마찬가지로 평균이 0이고 좌우 대칭입니다. t-분포를 따르는 확률 변수의 분산은 $\frac{\nu}{\nu-2}(\nu>2)$이라고 하는데 이 값은 1보다 큽니다. 따라서 표준 정규 분포보다는 봉우리가 낮고 양 끝이 높은 분포가 됩니다. 하지만 t-분포는 자유도가 커질수..

표본마다 분산이 같지는 않을테니 표본의 분산 역시 당연히 확률 변수입니다. 표본 분산을 $s^2$이라고 합시다. 표본 분산 $s^2$을 표본 평균의 분산 $Var(\overline{x})=\frac{\sigma^2}{n}$과 헷갈리면 안 됩니다. 표본 평균의 기대값이 모평균과 같듯이 표본 분산의 기대값도 모분산과 같아야 겠습니다.$$E(\overline{x})=E(x)=\mu$$$$E(s^2)=Var(x)=\sigma^2$$표본의 분산은 그냥 분산 공식에 따라 계산하면 되겠지라는 생각이 듭니다. 하지만 이렇게 구한 표본 분산은 확률 변수의 값들이 모평균이 아니라 표본 평균을 기준으로 흩어진 정도를 의미합니다. 그런데 표본 평균 자체가 모평균을 기준으로 흩어져 있습니다(#). 따라서 그 기대값은 모분산 보..

표본은 모집단에서 일부를 뽑아서 만든 집단입니다. 모집단을 모두 조사하는 것이 - 이론적으로든 현실적으로든 - 불가능한 경우에 표본 집단을 조사하여 모집단의 통계적 특성을 추정합니다. 하루에 수만개의 주사위를 생산하는 공장이 있습니다. 어떤 날에 만들어진 주사위가 제대로 만들어졌는지 - 어떤 눈이든 나올 확률이 6분의 1로 같은지 - 어떻게 확인할 수 있을까요?중심 극한 정리수만개를 일일이 다 조사하기에는 시간이 너무 많이 걸립니다. 그래서 주사위 30개를 뽑아서 한 번씩 굴려 보기로 했습니다. 이렇게 구한 30개의 숫자가 표본입니다. 이때 표본의 크기가 30이라고 합니다. 그리고 30개 숫자의 평균을 표본 평균이라고 합니다. 크기가 30인 표본을 만드는 방법은 굉장히 많고 표본마다 평균들이 같을 수가 ..

무한 주사위를 굴려서 나오는 숫자를 점으로 찍어 보면 점이 고르게 찍혔습니다. 어느 곳이든 확률 밀도가 $1\over{6}$로 동일했으니까요. 이런 분포를 균등 분포(uniform distribution)라고 합니다. 이제 무한 주사위를 30번 굴려서 나온 숫자들을 모두 더한 값을 생각해 봅시다. 이 값 역시 당연히 확률 변수입니다. 그리고 이 값들을 점으로 찍어 보았습니다. 점은 3천개, 칸의 너비는 3입니다.정규 분포의 확률 밀도 함수대충 보아도 가운데 부근의 밀도가 높고, 양 끝으로 갈수록 희박해지는 것 같습니다. 정확히 세어 보았습니다. 아래 표는 각 칸(bin)에 찍힌 점의 개수(count)와 확률(probability) 그리고 확률 밀도(probability density)를 보여 줍니다. 예..

들어가며통계학은 정말 다양한 분야에서 기본적인 연구 방법으로 사용되고 있는 것 같습니다. 그래서인지 이런 저런 연구를 살피다 보면 통계적 연구를 종종 접하게 됩니다. 통계학 그 자체에 관한 것이 아닌한에야 통계학 지식이 없어도 연구의 내용을 이해하는 것이 그리 어렵지는 않습니다. 하지만 통계학 지식이 조금이라도 있으면 연구의 내용을 더 잘 이해할 수 있지 않을까하는 아쉬움을 느끼곤 합니다. 그렇다고 본격적으로 통계학을 공부하는 것은 너무 부담스럽니다. 왜냐하면 직업적으로나 학문적으로나 통계학과는 거리가 먼 삶을 살고 있기 때문입니다. 그래서 부담스럽지 않은 수준으로 아쉬움을 달랠 정도로만 통계학 기초 지식을 몇 편의 글로 정리하기로 마음을 먹었습니다. 하지만 비전문가가 쓴 비전문적인 글이라서 엄정하지도 ..