들어가며
통계학은 정말 다양한 분야에서 기본적인 연구 방법으로 사용되고 있는 것 같습니다. 그래서인지 이런 저런 연구를 살피다 보면 통계적 연구를 종종 접하게 됩니다. 통계학 그 자체에 관한 것이 아닌한에야 통계학 지식이 없어도 연구의 내용을 이해하는 것이 그리 어렵지는 않습니다. 하지만 통계학 지식이 조금이라도 있으면 연구의 내용을 더 잘 이해할 수 있지 않을까하는 아쉬움을 느끼곤 합니다. 그렇다고 본격적으로 통계학을 공부하는 것은 너무 부담스럽니다. 왜냐하면 직업적으로나 학문적으로나 통계학과는 거리가 먼 삶을 살고 있기 때문입니다. 그래서 부담스럽지 않은 수준으로 아쉬움을 달랠 정도로만 통계학 기초 지식을 몇 편의 글로 정리하기로 마음을 먹었습니다. 하지만 비전문가가 쓴 비전문적인 글이라서 엄정하지도 않고 틀린 곳도 더러 있을 겁니다. 이점 꼭 유념하시고 가볍게 읽어 주시기를 바랍니다. 저와 비슷한 심정과 동기를 가지신 분들에게 도움이 되었으면 좋겠습니다.
주사위를 한 번 굴려서 나오는 수는 당연히 변수입니다. 1이 될 수도 있고 2 ~ 6이 될 수도 있기 때문입니다. 이 변수를 $x$라고 합시다. 주사위를 굴려서 1이 나올 확률이 곧 $x=1$이 될 확률입니다. 변수 $x$는 어떤 값을 갖든지 그 확률은 6분의 1로 같습니다. 이렇게 어떤 값이 나올 지는 모르지만 그 값이 확률적으로 결정되는 변수를 확률 변수(random variable)라고 합니다.
이산 확률 변수
확률 변수 $x$처럼 그 값들이 떨어져 있는 것을 이산 확률 변수(discrete random variable)라고 합니다. 값들이 떨어져 있다는 것은 어떤 두 값 사이에는 - 예컨데 1과 2 사이에는 - 값이 없는 경우가 있다는 말입니다. $x$축이 확률 변수의 값, $y$축이 확률이 되도록 그래프를 그려 보면 다음과 같습니다. 이 그래프를 확률 질량 함수(probability mass function)의 그래프라고 합니다.

연속 확률 변수
이제 눈이 12개인 주사위를 생각해 봅시다. 눈의 값은 각각 0.5, 1, 1.5, 2 ~ 6입니다. 이때 어떤 눈이 나올 확률은 $\frac{1}{12}$이 됩니다. 다시 눈의 개수를 2배로 늘려 봅시다. 눈의 값은 0.25, 0.5, 0.75 ~ 6이고 어떤 눈이 나올 확률은 $\frac{1}{24}$이 됩니다. 이런 식으로 눈이 계속 2배씩 늘어나서 개수가 무한대가 되면 어떤 눈이 나올 확률은 계속 반으로 줄어서 0에 수렴합니다.

눈의 개수가 무한대가 되면 어떤 두 값을 가져 오더라도 그 사이에 값이 있습니다. 이렇게 값들이 떨어져 있지 않고 이어져 있는 확률 변수를 연속 확률 변수(continuous random variable)라고 합니다. 그런데 연속 확률 변수의 확률 질량 함수는 아무런 의미가 없습니다. 모든 함수의 값이 0이기 때문입니다. 연속 확률 변수는 변수의 값이 어떤 특정한 범위에 있을 확률만 - 예컨대 2보다 작을 확률, 3보다 클 확률, 2와 3 사이에 있을 확률 등만 - 존재합니다.
확률 밀도 함수
눈의 개수가 무한대인 주사위를 - 일명 무한 주사위를 - 굴려 봅시다. 그리고 눈이 나올 때마다 사각형 안에 점을 찍어 봅시다. 사각형은 6개의 칸으로 나뉘어 있습니다. 각 칸의 너비는 모두 같습니다. 0 ~ 1 사이의 눈이 나오면 0 ~ 1 사이의 칸에 점을 찍는 식으로 눈과 대응하는 칸에 점을 찍어 보는 겁니다. 각 칸에 찍힌 점의 개수는 - 점을 충분히 많이 찍으면 - 모두 같다고 보아도 무방합니다. 다른 말로는 각 칸에 점이 찍힐 확률은 $\frac{1}{6}$ 정도로 모두 같다는 것입니다.
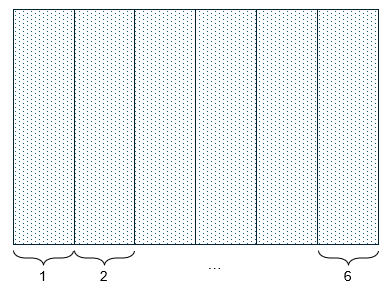
이제 6개의 칸 모두를 반으로 나누어 칸의 개수를 두 배로 늘려 봅시다. 각 칸에 찍힌 점의 개수는 반으로 줄어들 것입니다. 각 칸에 점이 찍힐 확률도 반으로 줄어 들어 $\frac{1}{12}$ 정도가 됩니다. 칸을 계속 절반으로 나누면 확률도 계속 반으로 줄어 들어 0에 수렴합니다. 하지만 칸의 너비도 계속 절반으로 줄어 들기 때문에 "너비 당 확률" 즉, 확률의 밀도는 변하지 않습니다.
사각형의 너비가 6이므로 칸의 개수를 $n$이라고 하면 칸의 너비는 $\frac{6}{n}$입니다. 한편 어떤 칸에 점이 찍힐 확률은 $\frac{1}{n}$입니다. 따라서 "너비 당 확률", 확률 밀도는 언제나 $\frac{1}{6} = \frac{1/n}{6/n}$입니다. 칸의 개수가 무한대가 되어서 $x$가 연속 확률 변수가 되더라도 확률 밀도는 변하지 않습니다. 따라서 확률 변수 $x$의 확률 밀도 함수(probability density function)는 이렇습니다.
$$
f(x)=\frac{1}{6}
$$
확률 밀도 함수의 그래프를 그려 보면 다음과 같습니다. 확률 밀도란 칸의 개수가 무한대일 때 즉, 칸의 너비가 0에 수렴할 때 "너비 당 확률"이 수렴하는 값을 말합니다. 아마도 앞에 나온 확률 질량 함수라는 이름은 확률 밀도 함수와의 일관성을 고려하여 붙인 이름인 듯 합니다. "부피 당 질량"이 밀도이기 때문입니다.

연속 확률 변수가 어떤 특정한 값을 가질 확률은 없다고 했습니다. 칸의 너비가 0이라면 그 칸에 찍힌 점도 없을테니 그 칸에 점이 찍힐 확률은 0이 되는 것입니다. 그렇다면 연속 확률 변수의 값이 특정 범위에 있을 확률 즉, 칸의 너비가 0이 아닐 때 그 칸에 점이 찍힐 확률은 어떻게 될까요? 확률 밀도가 "너비 당 확률"이므로 확률 밀도에 너비를 곱하면 확률이 됩니다. 따라서 $t$ ~ $t+1$ 사이에 점이 찍힐 확률은 $\frac{1}{6}=((t+1)-t)\cdot\frac{1}{6}$이 됩니다. 이는 확률 밀도 함수와 $x$축, 그리고 $t$ ~ $t+1$의 범위로 둘러 싸인 영역의 면적과 같습니다. 한편 확률 밀도 함수와 $x$축 그리고 전체 범위(0 ~ 6)로 둘러 싸인 영역의 면적 1이 됩니다. 확률을 모두 더하면 1이 되어야 하기 때문입니다.
'Building Block' 카테고리의 다른 글
| 통계학 겉 핥기 #6 - 회귀 분석 (0) | 2025.02.06 |
|---|---|
| 통계학 겉 핥기 #5 - 모평균의 추정 (0) | 2025.02.04 |
| 통계학 겉 핥기 #4 - 표본 분산 (0) | 2025.02.04 |
| 통계학 겉 핥기 #3 - 표본 평균 (0) | 2025.02.04 |
| 통계학 겉 핥기 #2 - 정규 분포 (0) | 2025.02.04 |