t-분포
확률 변수 $x$가 표준 정규 분포를 따르고, 확률 변수 $y$는 자유도가 $\nu$인 카이 제곱 분포를 따른다고 할 때, 확률 변수 $\frac{x}{\sqrt{y/\nu}}$는 자유도가 $\nu$인 t-분포(t-distribution)를 따른다고 합니다.
$$
x \sim N(0,1)
$$
$$
y \sim \chi_{\nu}^2
$$
$$t=\frac{x}{\sqrt{y/\nu}} \sim t_{\nu}
$$
t-분포는 표준 정규 분포와 마찬가지로 평균이 0이고 좌우 대칭입니다. t-분포를 따르는 확률 변수의 분산은 $\frac{\nu}{\nu-2}(\nu>2)$이라고 하는데 이 값은 1보다 큽니다. 따라서 표준 정규 분포보다는 봉우리가 낮고 양 끝이 높은 분포가 됩니다. 하지만 t-분포는 자유도가 커질수록 분산이 점점 작아지면서 1에 근접하므로 표준 정규 분포에 가까워집니다.
표본의 평균 $\overline{x}$가 정규 분포를 따르고, $\frac{(n-1)s^2}{\sigma^2}$이 카이 제곱 분포를 따른다면 다음 확률 변수 $t$는 자유도가 $(n-1)$인 t-분포를 따릅니다.
$$
\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}} \sim N(0,1)\
$$
$$
\frac{(n-1)s^2}{\sigma^2} \sim \chi_{n-1}^2
$$
$$
t=\frac{\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}}{\sqrt{\frac{\frac{(n-1)s^2}{\sigma^2}}{n-1}}}=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}} \sim t_{n-1}
$$
$t$ 값과 $z$ 값을 비교해보면 모분산 대신에 표본 분산을 사용한 것을 빼고는 동일합니다.
$$
z=\frac{\overline{x}-\mu}{\frac{\sigma}{\sqrt{n}}}$$
$$
t=\frac{\overline{x}-\mu}{\frac{s}{\sqrt{n}}}$$
모집단이 정규 분포가 아니더라도 중심 극한 정리에 따라 표본의 크기가 충분히 크면 표본의 평균 $\overline{x}$는 정규 분포를 따릅니다. 그러나 확률 변수 $\frac{(n-1)s^2}{\sigma^2}$는 모집단이 정규 분포일 때에만 카이 제곱 분포를 따릅니다. 그렇다면 모집단이 정규 분포가 아닐 때에는 t-분포를 이용할 수 없는 것일까요?
다행이도 모집단이 정규 분포가 아니더라도 t-분포를 이용할 수 있다고 합니다. 다만, 모집단의 분포가 너무 치우치지 않고 표본의 크기가 충분해야 한다고 합니다(#). 다시 주사위 공장으로 돌아가 봅시다. 주사위를 굴려서 나오는 수는 균등하게 분포하므로 정규 분포를 따르지 않습니다. 다만, 어느 한쪽으로 치우치지는 않았습니다. 따라서 표본의 크기가 충분하다면 t-분포를 이용할 수 있을 것 같습니다. 진짜로 그런지 확인해 봅시다.
주사위 30개를 뽑아서 한 번씩 굴려보고 표본을 만든 다음 표본 평균과 표본 분산을 구하여 t-값을 구해 보았습니다. 이렇게 구한 3천개의 t-값을 사용하여 확률 밀도 히스토그램을 그리고 그 위에 t-분포 곡선을 겹쳐 놓았습니다. 잘 들어 맞는습니다. 표본의 크기는 30이면 충분한 듯 합니다.
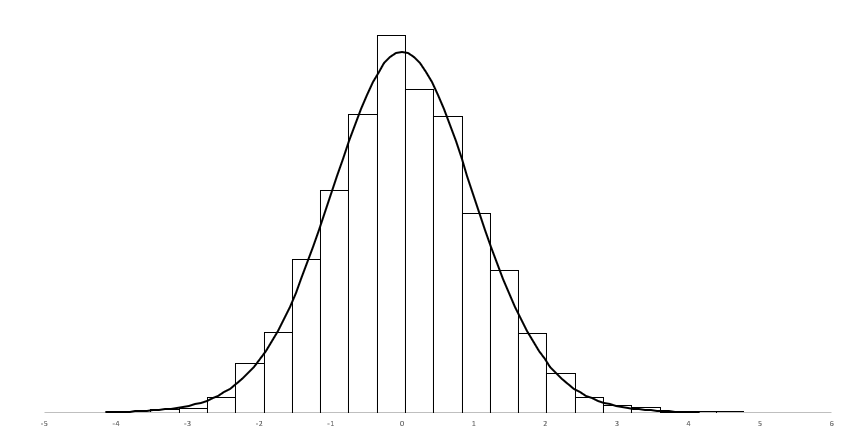
모평균의 추정
모집단이 정규 분포라면 표본의 크기가 아주 크지 않아도 표본 평균이 정규 분포가 된다고 하니 당연히 t-분포를 사용할 수 있습니다. 다음 그래프는 표준 정규 분포를 따르는 난수 5개를 뽑아서 만든 표본 1천개의 히스토그램입니다. 그리고 그 위에 정규 분포를 겹쳐 그렸습니다. 표본의 크기가 5개 밖에 되지 않아도 얼추 맞아 들어 갑니다.
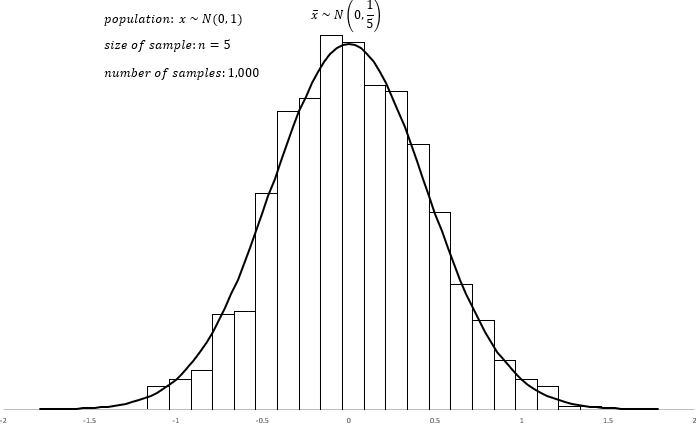
한편 모집단이 정규 분포가 아니더라도 표본이 충분히 크고 모집단의 분포가 너무 치우지지 않았다면 t-분포를 사용할 수 있다고 했습니다.
표본 조사를 통해 표본 평균과 표분 분산을 구하였다면 t-분포를 사용하여 모평균의 범위를 추정할 수 있습니다. 아래 그래프는 자유도가 29인 - 표본의 크기는 30인 - t-분포의 확률 밀도 함수입니다. 빗금 친 영역의 확률은 유의 수준 5%입니다. 따라서 신뢰 수준은 95%가 됩니다. 자유도가 29일 때 t-값이 평균을 기준으로 $\pm2.05$ 범위에 있을 확률이 95%이라는 겁니다.

그런데 모평균을 모르기 때문에 t-값을 구할 수는 없습니다. 그래서 한 가지 가정이 필요합니다. 일단 t-값이 흰색 영역에 들어간다고 가정하는 겁니다. 표본을 만들 때 모집단에서 흔한 것이 뽑히는 것이 보통이기 때문에 타당한 가정입니다.
표본 평균, 표본 분산을 구했고 신뢰 수준을 정했다면 아래와 같이 모평균 $\mu$의 범위를 추정할 수 있습니다. 신뢰 수준의 의미는 이런 식으로 100번 모평균을 추정한다면 확률적으로 95번은 실제 모평균이 추정 범위에 있을 것이고 그래서 추정을 95% 정도는 신뢰할 수 있다는 것입니다.
$$\begin{aligned}
p(-2.05<t<2.05)&=p(-2.05<\frac{\overline{x}-\mu}{s/\sqrt{n}}<2.05)\\
&=p(\overline{x}-2.05\cdot\frac{s}{\sqrt{n}}<\mu<\overline{x}+2.05\cdot\frac{s}{\sqrt{n}})\\
&=95\%
\end{aligned}$$
표본의 크기가 충분하다면 굳이 t-분포를 사용할 필요는 없습니다. 자유도 증가하면 t-분포는 표준 정규 분포에 근접하기 때문입니다. 아래 그래프를 보면 자유도가 29 정도 쯤 되면 표준 정규 분포와 거의 똑같아 보입니다. 따라서 표본의 크기가 충분히 크면 $t$ 값을 $z$ 값으로 보고 표준 정규 분포를 사용해도 됩니다.

z? t?
지난 포스팅에서는 z-값을, 이번에는 t-값을 사용하는 추정을 알아 보았습니다. 언제 z를 쓰고, 언제 t를 써야할까요?
모집단이 정규 분포라면 표본의 크기가 작아도 표본 평균은 정규 분포를 따고, $(n-1)s^2\over\sigma^2$도 카이 제곱 분포를 따릅니다. 따라서 모집단이 정규 분포라면 표본의 크기가 크든지 작든지 z-값, t-값 모두 사용할 수 있습니다.
하지만 모집단이 정규 분포가 아니라면 표본의 크기가 충분히 커야합니다. 그래야 중심 극한 정리에 따라 표본 평균이 정규 분포가 되고, $(n-1)s^2\over\sigma^2$도 카이 제곱 분포가 될 수 있기 때문입니다(물론 분포가 너무 치우쳐 있어서도 안됩니다). 따라서 모집단이 정규 분포가 아니라면 표본의 크기가 충분히 커야 z-값이나 t-값을 사용할 수 있습니다.
다만, z-값은 모분산을 알야야 구할 수 있을테니 그렇지 않다면 t-값을 사용해야 합니다. 모평균도 모르는데 모분산을 알 수 없는 경우가 대부분일 겁니다. 그래서 t-값을 많이 쓰게 될 것 같습니다.
z-값을 알면 표준 정규 분포, t-값을 알면 t-분포를 이용하여 추정을 합니다. 한편 표본의 크기가 충분히 크다면 t-분포가 정규 분포에 수렴하기 때문에 t-값을 z-값으로 간주하고 표준 정규 분포를 사용해도 됩니다.
'Building Block' 카테고리의 다른 글
| 통계학 겉 핥기 #7 - 회귀 모형의 검정 (2) | 2025.02.06 |
|---|---|
| 통계학 겉 핥기 #6 - 회귀 분석 (0) | 2025.02.06 |
| 통계학 겉 핥기 #4 - 표본 분산 (0) | 2025.02.04 |
| 통계학 겉 핥기 #3 - 표본 평균 (0) | 2025.02.04 |
| 통계학 겉 핥기 #2 - 정규 분포 (0) | 2025.02.04 |