회귀 분석(regression analysis)은 두 변수들 사이의 확률적 관계를 알아 보는 분석입니다. 알아 보려는 그 관계가 선형이라면 선형(linear) 회귀 분석이라고 합니다. 두 변수 $x$와 $y$가 완벽한 선형의 관계라면 $y=\beta_0+\beta_1x$의 꼴로 표현할 수 있겠습니다. 그런데 $x$와 $y$가 확률적 관계라면 $y$ 값은 확률적으로 결정될 것이고 완벽한 선형일 때와 비교하면 오차(error)가 있을 겁니다. 따라서 두 변수의 관계는 다음의 모형으로 표현할 수 있습니다.
$$
y=\beta_0+\beta_1x+\varepsilon
$$
여기서 $\varepsilon$이 오차를 의미하는 확률 변수입니다. $\varepsilon$은 엡실론이라고 읽습니다. $x$가 어떤 값이 되든 오차의 평균은 0, 분산은 $\sigma^2$으로 동일하다고 가정합니다.
$$
E(\varepsilon)=0
$$
$$
Var(\varepsilon)=\sigma^2
$$
$\varepsilon$이 확률 변수라서 $y$도 확률 변수가 됩니다. 그런데 $x$는 확률 변수가 아니라고 합니다(#). 회귀 분석은 $x$를 알고 있을 때 $y$의 값을 어느 정도의 오차를 감안하여 예측할 수 있는 모형을 만드는 작업입니다. 독립 변수 $x$는 사전적으로는 그 값이 확률적일 수 있겠지만 실현되어 관찰된 값은 불확실성이 없는 확정된 값입니다. 회귀 분석에서 독립 변수 $x$는 언제나 관찰되어 알려진 값이므로 상수와 다를 바가 없습니다.
$$
E(x)=x$$
$$Var(x)=0
$$
$\varepsilon$과 $x$의 평균과 분산이 저렇다면 어떤 주어진 $x$에 대하여 확률 변수 $y$의 기대값과 분산은 이렇게 됩니다(주석(1)).
$$
E(y)=\beta_0+\beta_1x
$$
$$
Var(y)=\sigma^2
$$
한편 오차 $\varepsilon$은 정규 분포를 따른다고 가정합니다. 따라서 $y$도 정규 분포를 따르게 됩니다. 선형 회귀 분석은 결국 $\beta_0$와 $\beta_1$를 알아 내는 것입니다. 하지만 모집단을 전수 조사하는 것은 현실적으로 불가능한 경우가 보통입니다. 따라서 표본 조사를 통하여 $\beta_0$와 $\beta_1$의 값을 추정하게 됩니다.

최소제곱법
아래 그래프에서 10개의 검은 점은 관찰된 표본입니다. 얼핏 보아도 우상향하는 추세를 쉽게 확인할 수 있습니다. 회귀 분석은 관찰된 변수 $x$와 $y$의 관계를 가장 잘 설명하는 회귀선을 찾는 것으로 시작합니다. 문자 위의 삿갓은 햇(hat)이라고 읽습니다.
$$
\widehat{y}=\widehat{\beta}_0+\widehat{\beta}_1x
$$
$\widehat{\beta}_0$과 $\widehat{\beta}_1$은 각각 $\beta_0$와 $\beta_1$의 추정치입니다. 과연 이 추정을 신뢰할 수 있는지는 검정을 해보아야 됩니다. 회귀 분석의 검정에 대하여는 다음 포스팅에서 알아 보겠습니다.

위의 그래프에서 관찰된 값 $y_i$와 예측된 값 $\widehat{y}_i$의 차이 $E$를 잔차(residual)라고 합니다. 잔차가 작을수록 회귀선은 관찰된 값에 가까워집니다. 그러나 잔차의 합계가 0이 되는 직선이 곧 회귀선은 아닙니다. 표본의 평균점 $(\overline{x}, \overline{y})$을 지나기만 한다면 그 어떤 직선도 잔차의 합계를 0으로 만들기 때문입니다. 그래서 회귀선은 최소제곱법(method of least squares)으로 찾는다고 합니다. 최소제곱법은 잔차의 제곱합 $\sum(y_i-\widehat{y}_i)^2$이 최소가 되는 회귀선을 찾는 방법입니다. 이 방법으로 찾은 $\widehat{\beta}_1$과 $\widehat{\beta}_0$은 - 즉, 회귀선의 기울기와 $y$ 절편은 - 다음과 같습니다(#).
$$\begin{aligned}
\widehat{\beta}_1&=\frac{\sum(x_i-\overline{x})(y_i-\overline{y})}{\sum(x_i-\overline{x})^2}\\
\\
\widehat{\beta}_0&=\overline{y}-\widehat{\beta}_1\overline{x}
\end{aligned}$$
그런데 $\widehat{\beta}_0$를 들여다 보면 평균점 $(\overline{x}, \overline{y})$이 회귀선 위에 있다는 사실을 알 수 있습니다.
$$
\overline{y}=\widehat{\beta}_0+\widehat{\beta}_1\overline{x}
$$
공분산
최소제곱법으로 회귀선을 구하려면 어려운 미분을 해야 합니다. 하지만 미분을 몰라도 직관적으로 이해할 수는 있을 것 같습니다. 아래 그림에서 회색 사각형들의 면적 평균값을 공분산이라고 합니다. 그래서 공분산을 구하는 식은 이렇습니다.
$$
Cov(x,y)=\frac{\sum(x_i-\overline{x})(y_i-\overline{y})}{n-1}$$
그래서 $\widehat{\beta}_1$은 공분산을 $x$의 분산으로 나눈 값이 됩니다.
$$\begin{aligned}
\widehat{\beta}_1&=\frac{\sum(x_i-\overline{x})(y_i-\overline{y})}{\sum(x_i-\overline{x})^2}\\
&=\frac {\frac{\sum(x_i-\overline{x})(y_i-\overline{y})}{n-1}} {\frac{\sum(x_i-\overline{x})^2}{n-1}}\\
&=\frac{Cov(x,y)}{Var(x)}
\end{aligned}$$
평균점을 기준으로 1, 3사분면에 있는 회색 사각형의 면적은 양수이고 2, 4사분면에 있으면 음수가 됩니다. 따라서 분포가 우상향하는 경우 음수인 부분보다 양수인 부분의 면적이 커서 공분산은 양수가 됩니다. 반대로 공분산이 음수이면 분포가 우하향하며, 관찰 값들이 여기 저기 산재하여 분포의 방향성이 없는 경우에는 면적이 상쇄되어 0에 가까워집니다. 공분산의 부호가 $\widehat{\beta}_1$의 부호와 같다는 말입니다. 그러나 공분산의 크기가 곧 $\widehat{\beta}_1$의 크기를 의미하지는 않습니다. 그렇다면 분포가 기운 정도를 의미하는 것은 무엇일까요?
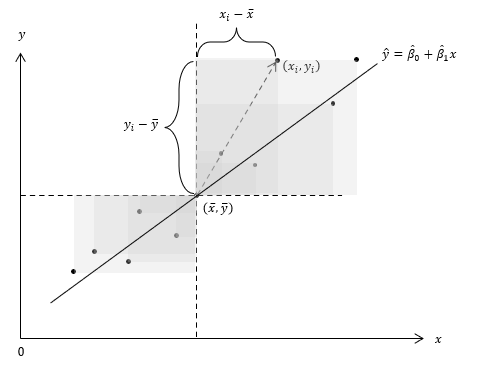
다시 위의 그림을 봅시다. 공분산은 회색 사각형들의 면적 평균값이라고 했습니다. 이 평균 면적과 면적이 동일한 가상의 사각형을 생각해 봅시다. 아마도 이 가상의 사각형의 대각선 기울기가 분포가 기운 정도일 것 같습니다. 그런데 사각형의 면적이 주어졌을 때 대각선의 기울기는 면적을 너비의 제곱으로 나누면 됩니다. 그리고 회색 사각형의 너비 제곱, $(x_i-\overline{x})^2$의 평균값은 곧 분산이므로 기울기는 공분산을 분산으로 나눈 값이 됩니다.
결정 계수
아래 그림에서 평균점 $(\overline{x}, \overline{y})$을 지나고 $x$축과 평행한 점선은 $x$와 $y$가 아무런 관계가 없음을 의미합니다. $x$가 어떻게 되든지 $\widehat{y}=\overline{y}$이기 때문입니다. 만약 최소제곱법으로 구한 회귀선이 누워서 점선에 가까워지면 $R$이 줄어 들고 잔차 $E$가 커집니다. 잔차가 커진다는 것은 회귀선의 설명력이 떨어진다는 말입니다. 반대로 잔차가 작아지면 회귀선의 설명력이 올라갑니다.
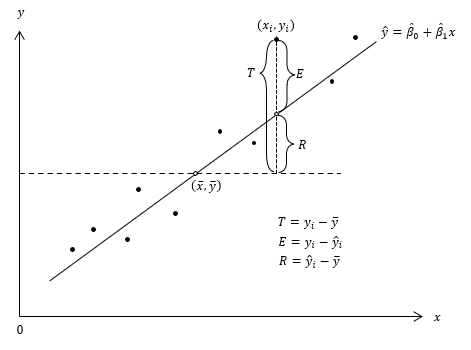
T, R, E의 제곱합을 각각 SST, SSR, SSE 라고 합시다. T, R, E의 단순 합은 0이기 때문에 제곱합을 사용합니다. 이때 회귀선의 설명력은 SST 대비 SSR의 비율로 정의할 수 있습니다. 이 비율을 결정계수(coefficient of determination)라고 합니다.
$$\begin{aligned}
SST&=\sum(y_i-\overline{y})^2\\
SSR&=\sum(\widehat{y}_i-\overline{y})^2\\
SSE&=\sum(y_i-\widehat{y}_i)^2
\end{aligned}$$
$$
R^2=\frac{SSR}{SST}
$$
그런데 독립 변수가 $x$ 하나 뿐인 단순 선형 회귀 분석에서는 SST=SSR+SSE 가 성립한다고 합니다(#). 따라서 결정계수는 이렇게 됩니다.
$$
R^2=\frac{SSR}{SST}=1-\frac{SSE}{SST}$$
회귀선이 완전히 누워서 $x$축과 평행하게 되면 결정계수는 0, 회귀선이 모든 점 $(x_i, y_i)$를 지나게 되면 1이 됩니다. 따라서 결정계수가 1에 가까울 수록 관측 값들이 회귀선 근처에 몰려 있게 됩니다.
상관 계수
공분산은 단위에 의존적인 값이라 비교가 용이하지 않습니다. 체중과 신장의 공분산은 신장의 단위가 센티미터인 경우에 미터일 때보다 100배가 더 큽니다. 단위와는 무관한 값이 되도록 공분산을 표준화한 값을 상관 계수(correlation coefficient)라고 합니다.
확률 변수 $x$와 $y$를 표준화한 확률 변수를 $u$, $v$라고 할 때 상관 계수는 $u$, $v$의 공분산이 됩니다. 그리고 상관 계수 $\rho$의(로라고 읽습니다) 범위는 $-1 \leq \rho \leq 1$ 입니다(#). 상관 계수가 양수이면 분포가 우상향하고 음수이면 우하향합니다. 그리고 0에서 멀어질수록 분포는 직선화가 됩니다.
$$
u=\frac{x-\overline{x}}{\sigma_x},v=\frac{y-\overline{y}}{\sigma_y}$$
$$
\overline{u}=\overline{v}=0, \sigma_u=\sigma_v=1$$
$$\begin{aligned}
Cov(u,v)&=\sum\frac{(u-\overline{u})(v-\overline{v})}{n}\\
&=\sum\frac{(\frac{x-\overline{x}}{\sigma_x}-0)(\frac{y-\overline{y}}{\sigma_y}-0)}{n}\\
&=\frac{\sum(x-\overline{x})(y-\overline{y})}{n\sigma_x\sigma_y}\\
&=\frac{Cov(x,y)}{\sigma_x\sigma_y}=\rho_{xy}
\end{aligned}$$
결론적으로 상관 계수는 두 변수의 공분산을 각각의 표준 편차로 나눈 값과 같습니다. 한편, 결정계수는 $x$와 $y$의 상관계수의 제곱이 됩니다(#).
$$\begin{aligned}
R^2&=\frac{\sum(\widehat{y}_i-\overline{y})^2}{\sum(y_i-\overline{y})^2}\\
&=\frac{\widehat{\beta}_1\sum{(x_i-\overline{x})(\widehat{y}_i-\overline{y})}}{\sum(y_i-\overline{y})^2}\\
&=\frac{Cov(x,y)^2}{\sigma_x^2\sigma_y^2}\\
&=\left(\frac{Cov(x,y)}{\sigma_x\sigma_y}\right)^2=\rho_{xy}^2
\end{aligned}$$
또한 회귀 계수는 상관 계수를 사용하여 이렇게 쓸 수 있습니다.
$$
\widehat{\beta}_1=\frac{Cov(x, y)}{Var(x)}=\frac{\rho_{xy}\sigma_x\sigma_y}{\sigma_x^2}=\rho_{xy}\cdot\frac{\sigma_x}{\sigma_y}
$$
조정 결정 계수
결정 계수는 독립 변수의 개수가 증가할수록 커지기만 합니다. 이를 두고 감소하지 않는 결정 계수의 속성이라고 합니다(non-decreasing property of R square)(#). 그래서 독립 변수가 많을수록 결정 계수가 과대 평가되어 있을 가능성이 높습니다. 한편 표본의 크기가 커질수록 결정 계수의 신뢰성은 당연히 올라갈 것입니다. 따라서 독립 변수의 개수와 표본의 크기를 고려하여 결정 계수를 조정할 필요가 있습니다. 조정 결정 계수(adjusted coefficient of determination)는 다음과 같이 계산합니다. $n$은 표본의 크기, $k$는 독립 변수의 개수입니다.
$$R_{adjusted}^2=1-\frac{(1-R^2)(n-1)}{(n-k-1)}
$$
독립 변수의 개수가 많을수록 조정 결정 계수는 작아지고 표본의 크기가 커질수록 조정 결정 계수는 결정 계수에 근접함을 알 수 있습니다. 독립 변수가 하나 뿐인 경우에는 - 단순 선형 회귀 분석에서는 - 조정 결정 계수와 결정 계수는 동일합니다.
'Building Block' 카테고리의 다른 글
| 통계학 겉 핥기 #7 - 회귀 모형의 검정 (2) | 2025.02.06 |
|---|---|
| 통계학 겉 핥기 #5 - 모평균의 추정 (0) | 2025.02.04 |
| 통계학 겉 핥기 #4 - 표본 분산 (0) | 2025.02.04 |
| 통계학 겉 핥기 #3 - 표본 평균 (0) | 2025.02.04 |
| 통계학 겉 핥기 #2 - 정규 분포 (0) | 2025.02.04 |