horust

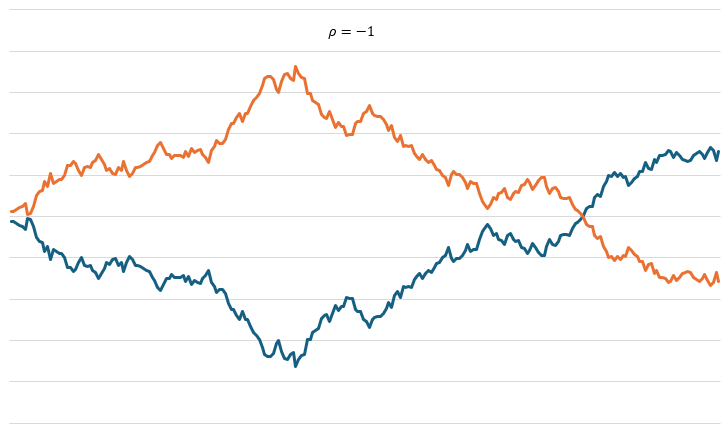
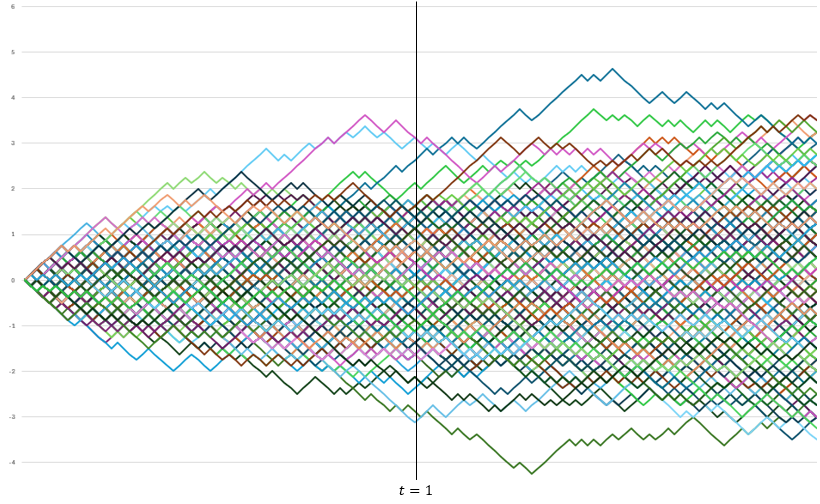
모든 주식의 수익율이 완전히 따로 놀지는 않습니다. 어떤 주식끼리는 같은 방향으로 움직이기도 하고, 또 어떤 주식들은 서로 다른 방향으로 움직이기도 할 겁니다. 주식 A의 수익율이 브라운 운동을 한다고 가정하면 주가의 흐름을 만들어 낼 수 있습니다. 주식 B도 마찬가지입니다. 그런데 이렇게 만들어 낸 주가의 흐름은 서로 아무런 관련이 없습니다. 만약 주식 A와 B의 수익율 간에 어떤 상관 관계가 있다면 주가의 흐름들도 이를 반영할 수 있어야 합니다.분산-공분산 행렬확률 변수들 사이의 공분산은 행렬로 표현할 수 있습니다. 다음은 세 개의 확률 변수 $X_1$, $X_2$, $X_3$ 사이의 공분산을 나타낸 행렬입니다. $Cov(a,b)=Cov(b,a)$이므로 좌상에서 우하로 그은 대각선을 기준으로 상하 대..

지난 포스팅에서 무작위 보행 함수는 모든 함수의 값이 확률 변수라는 것을 알았습니다. 이런 함수를 확률 함수라고도 하고 확률 과정이라고도 한다고 했습니다. 그리고 평균과 분산도 구해 보았습니다. 그런데 무작위 보행 함수는 어떤 확률 분포를 따르게 될까요?무작위 보행의 확률 분포무작위 보행 함수 $W_n(t)$의 그래프를 그려 보았습니다. 단면을 잘라 보면 $W_n(t)$의 확률 분포를 가늠할 수 있을 겁니다. 아래 그래프는 시간 당 64 걸음씩, 2시간 동안, 255번을 무작위로 걸어 본 결과입니다. 점과 점의 사이 사이는 보간법으로 집어 넣었습니다.$t=1$ 시점의 단면을 잘라서 얻은 $W_{64}(1)$의 값 255개로 히스토그램을 그려 보았습니다. 히스토그램과 겹쳐 놓은 그래프는 정규 분포의 확률 ..