들어가며
약 200년 전에 스코틀랜드의 식물학자 로버트 브라운(Robert Brown)은 물 속에서 꽃가루 입자들이 불규칙하게 움직이는 현상을 처음으로 진지하게 연구했다고 합니다. 물의 흐름이 없는데도 꽃가루 입자들은 이리 저리 움직입니다. 나중에 밝혀졌는데 이 현상은 물 분자와 꽃가루 입자의 충돌 때문입니다. 물 분자들이 어디서 달려와 부딪힐 지 모르니 꽃가루의 움직임이 불규칙한 것입니다. 이를 이론적으로 정립한 분이 그 유명한 알버트 아인슈타인(Albert Einstein)입니다. 그리고 또 시간이 흘러 노버트 위너(Norbert Wiener)라는 분이 브라운 운동을 수학적으로 정의했다고 합니다. 그래서 물 속의 꽃가루 움직임처럼 무작위적인 움직임을 브라운 운동 또는 위너 과정이라고 부릅니다. 그리고 또 시간이 지나 브라운 운동은 주가의 움직임을 설명하는 모형으로 사용되기 시작했습니다. 그 유명한 블랙-숄즈 모형(Black-Scholes Model)도 브라운 운동에 기반하고 있다고 합니다.
오늘날 주가의 움직임을 설명하는 모형으로 가장 널리 사용되는 것은 기하 브라운 운동이라고 합니다. 투자 전략을 세웠으면 미래 수익을 가늠해 보아야 할텐데요. 그럴러면 그럴싸한 주가 흐름을 만들어 내야 합니다. 그리고 앞으로 어떤 상황이 올 지 모르니 다양한 주가 흐름을 만들어 보아야 할 겁니다. 이때 기하 브라운 운동이 큰 도움을 줍니다. 사실 공식만 알고 있어도 주가 흐름은 만들어 낼 수 있습니다. 하지만 언제나 그렇듯이 아쉬움이 남습니다. 브라운 운동을 조금이나마 이해한다면 주가의 움직임을 더 잘 이해할 수 있지 않을까하는 아쉬움 말이죠. 하지만 막상 들여다 보고 나면 엄청난 후회가 밀려 옵니다. 사실 브라운 운동은 아주 난해한 수학의 향연입니다. 그렇다고 이제와서 수학을 배울 수도 없는 노릇입니다. 솔직히 능력도 안되거니와 배우고 싶지도 않습니다. 하지만 모든 것을 꼭 제대로 이해해야만 하는 것은 아닙니다. 사람은 무엇을 이해하면서 즐거움을 얻습니다. 수학을 모른다고 이런 즐거움을 포기할 수는 없습니다.
일단 꽃가루에서 시작합시다. 물속의 꽃가루가 어디로 움직일 지는 예측할 수 없습니다. 비틀거리는 만취한 사람의 걸음걸이처럼 말이죠. 이렇게 다음 발자국이 놓일 곳을 예상할 수 없는 걸음을 무작위 보행(random walk)이라고 합니다. 그렇다면 동전을 던진 결과에 따라 걸어 보는 것도 무작위 보행이 됩니다. 다음에 어느 면이 나올지 알 수 없으니까요. 이렇게 한동안 걷다가 도착하게 될 곳은 동전의 앞면과 뒤면이 나온 회수에 따라 달라질 겁니다.
1-차원 단순 대칭 무작위 보행
동전을 던져서 앞면이 나오면 $a$만큼, 뒷면이 나오면 $b$만큼 걸어 보기로 하겠습니다. $a$나 $b$가 양수면 앞으로, 음수면 뒤로 가는 겁니다. $a=b$라면 무작위 보행이 아니므로 $a>b$라고 가정합니다. $a$나 $b$의 단위가 무엇이든 - 환산이 가능하므로 - 상관은 없지만 설명의 편의 상 걸음이라고 하겠습니다.
동전을 던져서 앞면이나 뒷면이 나올 확률은 $1\over{2}$로 같습니다. 따라서 동전을 한 번 던졌을 때 위치의 변화량을 $y$라고 하면 그 확률 분포 및 평균($m$)과 분산($s^2$) 그리고 표준 편차($s$)는 다음과 같습니다.
$$\begin{aligned}
&p(y=a)=p(y=b)=\frac{1}{2}\\
\\
&m=E(y)=\frac{1}{2} \cdot a + \frac{1}{2} \cdot b = \frac{a+b}{2}\\
\\
&s^2=Var(y)=\frac{1}{2} \cdot \left(a- \frac{a+b}{2}\right)^2 + \frac{1}{2} \cdot \left(b- \frac{a+b}{2}\right)^2=\left(\frac{a-b}{2}\right)^2\\
\\
&s=\frac{a-b}{2}\quad\because a>b
\end{aligned}$$
표준화
어떤 확률 변수에서 평균을 빼고 표준 편차로 나누어 새로운 확률 변수를 정의하는 과정을 표준화(standardization)라고 합니다. 이 과정을 표준화라고 부르는 이유는 이렇게 정의된 확률 변수는 언제나 평균이 0, 분산은 1이 되기 때문입니다. $y$를 표준화한 확률 변수를 $x$라고 합시다.
$$x=\frac{y-m}{s}
$$
$$E(x)=E\left(\frac{y-m}{s}\right)=\frac{E(y)-m}{s}=0
$$
$$Var(x)=Var\left(\frac{y-m}{s}\right)=\frac{Var(y)}{s^2}=1
$$
$y=a$이면 $x=1$이고, $y=b$이면 $x=-1$이므로 $x$의 확률 분포는 이렇게 됩니다.
$$p(y=a)=p\left(x=\frac{a- \frac{a+b}{2}}{\frac{a-b}{2}}\right)=p(x=1)=\frac{1}{2}
$$
$$p(y=b)=p\left(x=\frac{b- \frac{a+b}{2}}{\frac{a-b}{2}}\right)=p(x=-1)=\frac{1}{2}
$$
$$\therefore p(x=1)=p(x=-1)=\frac{1}{2}
$$
그런데 $x$의 확률 분포를 보면 동전을 던져서 앞면이 나오면 앞으로 한 걸음, 뒷면이 나오면 뒤로 한 걸음 걷는 무작위 보행의 확률 분포와 같습니다. 이렇게 동전을 던져서 나온 면에 따라 앞이나 뒤로(1-dimensional) 한 걸음만(simple) 갈 수 있고 그 확률은 동일한(symmetric) 걸음을 1-차원 단순 대칭 무작위 보행이라고 합니다. 어디로 얼마만큼 걷게 되든지 무작위 보행은 이렇게 표준화할 수 있습니다.
줄인 무작위 보행
모든 무작위 보행을 표준화할 수 있으니 $a$와 $b$가 어떻게 되든지 신경 쓰지 않아도 됩니다. 이제부터는 앞이나 뒤로 한 걸음만 간다고 생각하면 됩니다. 하지만 아직 신경 쓸 일이 하나 남아 있는데 그것은 시간입니다. 달리 말하자면 사람마다 걷는 속력은 다를 수 있다는 겁니다. 똑같이 10 걸음을 걸어도 한 시간이 걸린 것과 30분이 걸린 것은 다릅니다.
한 시간에 $n$ 걸음을 걸어 보겠습니다. 꼭 한 시간일 필요는 없습니다. 하루, 한달, 일년 등 어떤 시간 단위여도 상관 없지만 설명의 편의 상 시간 단위는 한 시간으로 하겠습니다. 앞으로 가든 뒤로 가든 한 시간에 $n$ 걸음이니 $n$이 곧 시속입니다. 동전을 던질 때마다 한 걸음이니 $n$은 한 시간에 동전을 던진 회수이기도 합니다. 한 시간 동안 동전을 $n$번 던져서 나오는 $x$의 값들을 차례대로 $x_1$, $x_2$, ..., $x_n$이라고 합시다. 동전을 $n$번 던지고 난 후의 위치를 $S_n$이라고 하면, $S_n$은 $x_1$부터 $x_n$을 모두 더한 값이 됩니다. 출발점은 0이라고 가정하겠습니다. 이렇게 가정하면 $S_n$은 출발 후 첫 1 시간 후의 위치이자, 첫 1 시간 동안 위치의 변화량이기도 합니다.
$$\begin{aligned}
S_0&=0\\
S_1&=S_0+x_1=x_1\\
S_2&=S_1+x_2=x_1+x_2\\
&...\\
\therefore S_n&=x_1+x_2+...+x_n=\sum{x_i}
\end{aligned}$$
예컨대, 동전을 4번 던져서 순서대로 H(앞면), H, T(뒷면), H이 나왔다면 $S_n=1+1-1+1=2$가 됩니다. 하지만 $S_n$은 0, 4, -2, -4가 될 수도 있었습니다. $x$가 확률 변수이므로 $S_n$도 확률 변수가 되는 것입니다. $S_n$의 확률 분포를 그래프로 나타내자면 다음과 같습니다. 출발점(0)을 기준으로 완벽한 대칭입니다.

그런데 동전을 던졌을 때 나오는 면은 그 이전에 나왔던 것과도, 앞으로 나올 것과도 아무런 관계가 없습니다. 이렇게 서로 아무런 관계가 없는 것을 독립적이라고 합니다. 그리고 동전이 찌그러지지 않은 한 몇 번을 던져도 확률은 동일할 겁니다. 따라서 모든 $x_i$들은 서로 독립적이며 동일한 분포(Independent and Identically Distributed, i.i.d)를 따릅니다. 모든 $x_i$들이 $i.i.d$이므로 $S_n$의 분산도 - 평균을 구할 때와 마찬가지로 - $x_i$들의 분산을 모두 더해서 구할 수 있습니다.
$$E(S_n)=E\left(\sum{x_i}\right)=\sum{E(x_i)}=0\quad\because E(x_i)=0
$$
$$Var(S_n)=Var\left(\sum{x_i}\right)=\sum{Var(x_i)}=n\quad\because Var(x_i)=1
$$
$S_n$의 분산은 속력 그 자체입니다. 따라서 $n$이 커질수록 출발점에서 평균적으로 멀리 떨어지게 됩니다. 하지만 표준화를 하고나면 떨어진 정도 즉, 분산은 언제나 1이 됩니다.
$$\frac{S_n-E(S_n)}{\sqrt{Var(S_n)}}=\frac{S_n}{\sqrt{n}}
$$
$$E\left(\frac{S_n}{\sqrt{n}}\right)=\frac{E(S_n)}{\sqrt{n}}=0\quad\because E(S_n)=0
$$
$$Var\left(\frac{S_n}{\sqrt{n}}\right)=\frac{Var(S_n)}{n}=1\quad\because Var(S_n)=1
$$
그런데 $S_n$은 모든 $x_i$를 더한 것이므로 $S_n$을 표준화한 것은 $x_i$의 크기를 $1\over\sqrt{n}$로 줄여서 모두 더한 것과 같습니다. 동전을 한 번 던졌을 때의 위치 변화량을 이런 식으로 조정한 것을 줄인 무작위 보행(scaled random walk)이라고 합니다. 빨리 걷는 대신에 보폭을 적당히 작게 줄였다고 생각하면 됩니다.
$$\begin{aligned}
\frac{S_n}{\sqrt{n}}&=\frac{x_1+x_2+...+x_n}{\sqrt{n}}\\
&=\frac{x_1}{\sqrt{n}}+\frac{x_2}{\sqrt{n}}...+\frac{x_n}{\sqrt{n}}\\
&=\displaystyle\sum_{i=1}^{n}\frac{x_i}{\sqrt{n}}
\end{aligned}$$
확률 과정
한 시간에 $n$ 걸음을 걷는다면 $t$ 시간 동안에는 $nt$ 걸음을 걷게 됩니다. 그리고 한 걸음을 옮길 때 위치 변화량이 이제 $\frac{x}{\sqrt{n}}$이므로 $t$ 시간 후의 위치는 이렇게 됩니다. $W_n(t)$를 무작위 보행 함수라고 합시다.
$$W_n(t)=\displaystyle\sum_{i=1}^{nt}\frac{x_i}{\sqrt{n}}=\frac{S_{nt}}{\sqrt{n}}
$$
그런데 1시간 미만 단위, 예컨데 1시간 30분($t=1.5$)이나 2시간 12분($t=2.2$) 후의 위치는 어떻게 될까요? 한 시간에 4 걸음을 걷는다면($n=4$) 1시간 30분은 딱 6 걸음입니다($nt=6$). 하지만 2시간 12분은 8.8 걸음이($nt=8.8$) 됩니다. 동전을 8.8번 던져야 하지만 0.8번을 던질 수는 없습니다. 따라서 위에서 정의한 무작위 보행 함수는 동전을 1번 미만으로 던지는 경우를 다룰 수 없습니다.
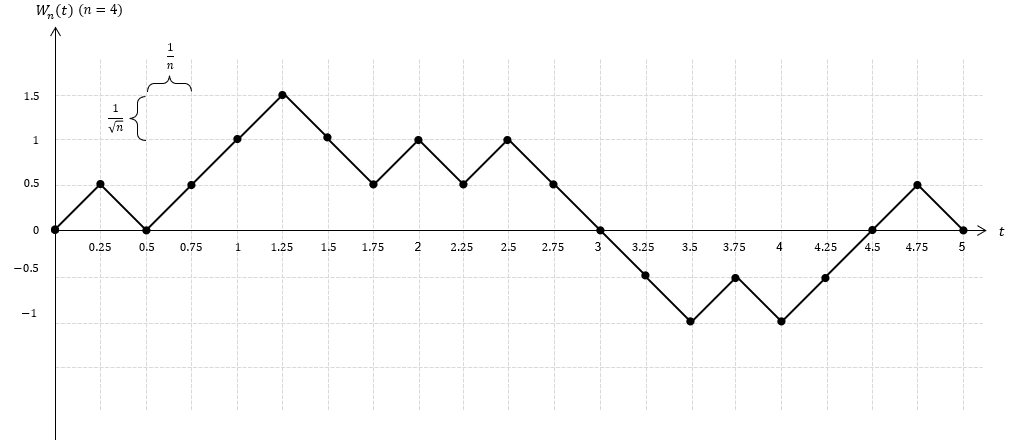
한 시간에 동전을 4번씩($n=4$), 5시간 동안($0\leq{t}\leq5$) 던져서 이 함수의 그래프를 직접 그려 보았습니다. 이 함수는 $nt$가 정수인 경우에만 값을 갖기 때문에 그래프는 선이 아닌 점으로 표시됩니다(주석 (1)). 점들은 특정 시점의 위치를 의미하므로 점을 따라가면 이동 경로가(path) 됩니다.

그런데 무작위 보행을 하면 이동 경로가 매번 같을 수가 없기 때문에 무작위 보행 함수는 그래프를 그릴 때마다 달라집니다. 이는 어떤 시점의 위치가 동전을 던져서 결정되기 때문에 당연한 결과입니다. 달리 말하자면 모든 함수 값들이 확률 변수라는 것입니다. 이런 함수를 확률 함수(random function)라고 합니다. 확률 함수의 모든 점들은 확률 변수들이라서 이 점들을 따라 가는 경로는 매번 달라질 수 밖에 없습니다. 경로는 위치가 변해가는 과정(process)이므로 확률 함수는 확률 과정(random process 또는 stochastic process)이라고도 합니다.
확률 변수 $W_n(t)$의 평균과 분산은 다음과 같습니다. 시간이 흘러가면서 분산이 커지기 때문에 확률 과정은 출발점에서 시작해서 확산되어(diffusion) 갑니다.
$$
E(W_n(t))=E\left(\frac{S_{nt}}{\sqrt{n}}\right)=\frac{E(S_{nt})}{\sqrt{n}}=0\quad\because E(S_{nt})=0$$
$$Var(W_n(t))=Var\left(\frac{S_{nt}}{\sqrt{n}}\right)=\frac{Var(S_{nt})}{n}=t\quad\because Var(S_{nt})=nt
$$
주석
(1) 무작위 보행 함수
무작위 보행 함수는 $nt$가 정수가 아닐 때에는 정의할 수 없습니다. 예를 들어 한 시간에 4 걸음을 걸으면($n=4$) 2시간 12분($t=2.2$) 후의 위치는 8.8 걸음($nt=8.8$)을 걸어 보아야 알 수 있습니다. 하지만 동전을 0.8번 던질 수는 없으니 동전을 1 번 미만으로 던져되는 경우에는 함수가 정의되지 않습니다.
계단 함수
그런데 다음 번 동전을 던질 때까지는 지금 위치에 그대로 머물러 있는 것으로 볼 수 있습니다. 예를 들어 $t=2.2$일 때에는 $t=2$ 시점의 위치에 머무르다가 $t=2.25$가 되어 동전을 던지면 그 때 움직인다고 보는 겁니다.

이렇게 가정하면 무작위 보행 함수는 위의 그래프에서 보듯이 계단 함수(step function)가 됩니다. ${\lfloor{\cdot}\rfloor}$은 내림(floor)를 말합니다. 예컨데 ${\lfloor{8.8}\rfloor}=8$이 됩니다.
$$W_n(t)=\displaystyle\sum_{i=1}^{\lfloor{nt}\rfloor}\frac{x_i}{\sqrt{n}}=\frac{S_{\lfloor{nt}\rfloor}}{\sqrt{n}}$$
보간법
또 다른 가정은 8.8 걸음을 8 걸음을 걸었을 때의 위치에다가 9번째 걸음의 0.8만큼 더한 것으로 보는 겁니다.
$$W_4(2.2)=\frac{S_8}{\sqrt{4}}+(8.8-8)\cdot\frac{x_9}{\sqrt{4}}
$$
점들의 사이 사이를 이런 식으로 보충하는 방법을 보간법(interpolation)이라고 합니다. 이를 일반화하면 무작위 보행 함수는 이렇게 정의됩니다.
$$W_n(t)=\frac{S_{\lfloor{nt}\rfloor}}{\sqrt{n}}+(nt-{\lfloor{nt}\rfloor})\cdot{\frac{x_{{\lfloor{nt}\rfloor}+1}}{\sqrt{n}}}$$
이렇게 가정하면 무작위 보행 함수는 점과 점을 이어 붙인 모습이 됩니다. 보간법으로 정의한 값들은 점과 점을 잇는 선 위에 있기 때문입니다.