풋 옵션
풋 옵션은 주식을 팔 수 있는 권리입니다. 콜 옵션과는 반대로 주가가 행사 가격보다 낮을수록 만기 가치가 커집니다. 예를 들어 1달이 지난 시점에 100원을 받고 주식 1주를 팔 수 있는 풋 옵션이 있다고 합시다. 한 달 후의 주가가 50원이 되었다면 이 옵션을 가진 사람은 권리를 행사할 겁니다. 100원을 받고 50원 짜리 주식을 팔면 50원 이득이기 때문입니다. 반면에 한 달 후의 주가가 200원이면 그냥 권리를 포기하는 것이 이득입니다. 200원 짜리 주식을 100원을 받고 팔 수는 없으니까요. 행사 가격($K$)이 만기 시점($t$)의 주가($S_t$) 보다 높은 만큼 이득이지만 행사 가격이 주가가 낮아도 높아도 손해는 없습니다. 따라서 만기 시점의 풋 옵션 가치는 이렇게 표현할 수 있습니다.
$$
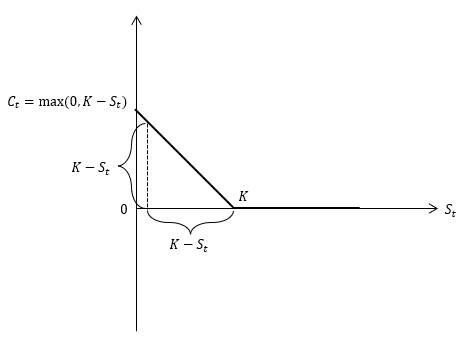
P_t=\max(0,K-S_t)
$$
그리고 이를 그래프로 그리면 다음과 같습니다.
풋-콜 패리티
콜 옵션의 가격을 구할 때와 마찬가지로 풋 옵션의 가격도 복제 포트폴리오를 만들어 구할 수 있습니다. 그때와 한 가지 다른 점은 가격이 알려진 자산이 하나 더 늘었다는 겁니다. 바로 콜 옵션입니다.
아래 그림은 주식, 예금 그리고 콜 옵션이라는 퍼즐로 풋 옵션의 복제 포트폴리오를 맞추는 방법을 설명하고 있습니다. 아래 그림에 나타난 각 그래프들은 옵션의 만기 시점에 주가에 따른 각 자산의 만기 가치를 나타냅니다. 먼저 콜 옵션을 하나 삽니다(1). 이 콜 옵션은 풋 옵션과 기초 자산, 행사 가격, 만기가 동일합니다. 그리고 예금을 넣습니다(2). 이 예금의 만기는 풋 옵션과 동일하고 만기 원리금은 행사 가격과 같습니다. 마지막으로 기초 자산과 동일한 주식을 한 주 빌려 옵니다(3).
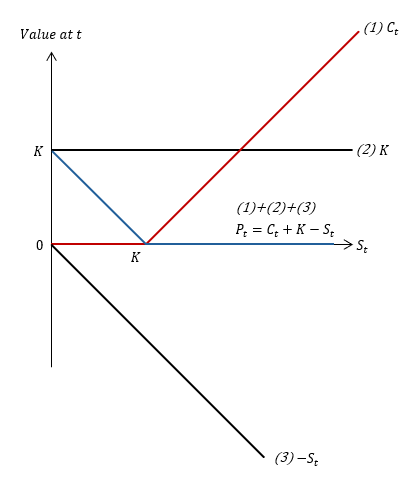
위의 그림에서 보듯이 풋 옵션 1주는 콜 옵션 1주와 예금 그리고 주식 1 주를 빚진 포트폴리오와 같습니다(1+2+3).
$$
P_t=C_t+K-S_t
$$
만기 가치가 같으니 현재 가치도 같아야 합니다. 이때 예금 이자율 $r$은 무위험 이자율입니다. 무위험 이자율이 되어야 하는 이유는 지난 포스팅을 참고 하시면 됩니다.
$$
P=C+Ke^{-rt}-S
$$
풋 옵션과 콜 옵션 가격 사이에는 성립하는 이와 같은 등가 관계를 풋-콜 패리티(put-call parity)라고 합니다.
이항 모형
동전을 $nt$ 던지면 앞면이 $a$번 이상 나오거나, $a$번 미만으로 나오거나 둘 중 하나입니다. 앞면이 $a$번 미만으로 나올 때 뒷면은 $nt-a$번 이상 나옵니다. 따라서 두 확률을 더하면 1이 되어야 합니다.
$$\begin{aligned}
p(j\geq a)+p(j<a)&=p(j\geq a)+p(nt-j\geq nt-a)\\
&=B(a;nt,p)+B(nt-a;nt,1-p)\\
&=1\\
\therefore B(nt-a;nt,1-p)&=1-B(a;nt,p)
\end{aligned}$$
이를 이용하면 풋 옵션의 가격은 이항 모형으로 아래와 같이 표현할 수 있습니다. 해보지는 않았지만 직접 유도해도 당연히 저렇게 되겠죠?
$$\begin{aligned}
P&=C+K^{-rt}-S\\
&=(S\cdot B(a;nt,\rho)-Ke^{-rt}\cdot B(a;nt,\pi))+Ke^{-rt}-S\\
&=Ke^{-rt}(1-B(a;nt,\pi))-S(1-B(a;nt,\rho))\\
&=Ke^{-rt}B(nt-a;nt,1-\pi)-SB(nt-a;nt,1-\rho)
\end{aligned}$$
블랙-숄즈 모형
정규 분포는 좌우 대칭이므로 $1-N(x)=N(-x)$가 됩니다. 아래 그림을 보면 쉽게 이해가 됩니다.

이러한 정규 분포의 대칭성, 풋-콜 패리티를 이용하면 블랙-숄즈의 공식으로 풋 옵션의 가격은 이렇게 표현됩니다.
$$\begin{aligned}
P&=C+Ke^{-rt}-S\\
&=(SN(d_1)-Ke^{-rt}N(d_2))+Ke^{-rt}-S\\
&=Ke^{-rt}(1-N(d_2))-S(1-N(d_1))\\
&=Ke^{-rt}N(-d_2)-SN(-d_1)
\end{aligned}$$